أسباب تسرب المياه من الثلاجة

إن بوابة AND المنطقية هي واحدة من البوابات المنطقية الأساسية ويطلق عليها بوابة الضرب المنطقي لذلك نجدها تدخل في العديد من الدوال، وسوف نقوم بشرحها بالتفصيل في السطور القادمة.

ماهي بوابة AND Gate المنطقية

تعرف البوابة AND بأنها عبارة عن دائرة إلكترونية تتعامل فقط مع الحالات المنطقية 0 أو 1 ويطلق عليها أيضا الضرب المنطقي، لها مدخلان أو أكثر و لها مخرج وحيد وتعمل وفق المبدأ الآتي:

 
يكون خرج البوابة AND في حالة (1) إذا كانت جميع المداخل لها في حالة (1)؛ويكون الخرج للبوابة AND في حالة (0) إذا كان احد المداخل لها في حالة (0).

الدائرة الكهربائية للبوابة AND

الدائرة الكهربائية للبوابة AND

لتوضيح عمل هذه البوابة اكثر نقوم بعمل الدائرة الكهربائية التالية:

ونلاحظ من الشكل السابق أن كلا من A و B يمثلان مفتاحين كهربائيين هما مدخلا البوابة، ويمثل المصباح (Lamp) مخرجها، إذا كان أي من المفتاحين أو كلاهما في حالة فصل OFF فلن يمر تيار كهربائي في الدائرة ولن يضئ المصباح الكهربائي، والحالة الوحيدة التي يمر فيها التيار الكهربائي هي عندما يكون كلا المفتاحين A و B مغلقين أي بحالة وصل ON.

رمز البوابة AND

رمز البوابة AND 

يكون مداخل البوابة هما A و B ومن الممكن أن تكون المداخل أكثر من مدخلين، ويتم الرمز بالخرج بالرمز Q؛ويتم القراءة Q تساوي A و B؛ويتم التعبير عنه بالرمز البوليني A  AND B حيث أن (.)=(AND) .

وظيفة البوابة AND

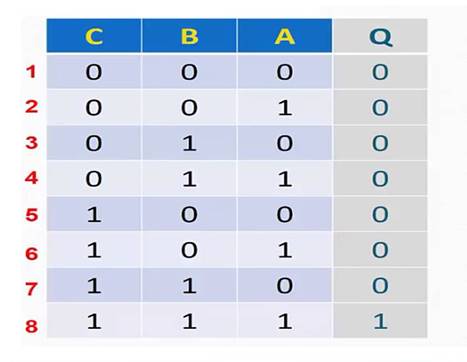
يمكننا التعرف على وظيفة البوابة AND من خلال جدول الحقيقة Truth Table، وجدول الحقيقة هذا يوضح لنا جميع الاحتمالات الممكنة للبوابة AND كما في الشكل التالي:

جدول الحقيقة Truth Table

جدول الحقيقة Truth Table

يمكننا ملاحظة أن غالبا يتم وضع أول مدخل A بعد خانة المخرج Q ثم خانة المدخل الثاني B؛يكون من السهل معرفة الاحتمالات الممكنة إذا كانت البوابة لها مدخلين ولكن إذا كانت البوابة لها أكثر من مدخلين كيف يمكن لنا تعبئة جدول الحقيقة ومعرفة الاحتمالات الممكنة بسهولة؟ يكون ذلك من خلال التالي:

عدد المداخل =n
عدد الاحتمالات(عدد الصفوف في جدول الحقيقة)=2ⁿ
فلو عندنا 3 مداخل تصبح n = 3
ويكون عدد الاحتمالات هي 2³=8 احتمالات (صفوف)
ولكن كيف يتم تعبئة هذه الصفوف في جدول الحقيقة؟
يتم رسم الجدول كالتالي:

رسم جدول الحقيقة فارغ

ونبدأ بالمدخل A نبدأ بالاحتمال (0) ثم الاحتمال 1 ونكرر هذا إلى الوصول إلى الاحتمال الأخير وهو (1).
ثم ننتقل إلى المدخل B نبدأ بالاحتمال (0) ثم الاحتمال (0) ثم الاحتمال (1) ثم الاحتمال (1) ونكرر هذا إلى الوصول إلى الاحتمال الأخير ويكون الاحتمال الأخير هو (1).
ثم ننتقل إلى المدخل C بما أن هذا النظام ثنائي نبدأ الاحتمالات بأربع احتمالات 0,0,0,0 ثم أربع 1,1,1,1 ثم نكرر هذا حتى الوصول إلى الاحتمال الأخير ويكون الاحتمال الأخير يساوي (1)أيضا.
يصبح الحصول على قيمة خانة الخرج Q أمرا سهلا حيث أن بوابة AND لا يكون الخرج فيها يساوي (1) إلا إذا كانت جميع المداخل بها تساوي (1) فتكون قيمة Q في جميع خانات الاحتمالات تساوي (0) ما عدا الاحتمال الأخير تكون قيمة Q تساوي (1).
وبذلك نكون قد قمنا بتعبئة جدول الحقيقة بمنتهي السهولة كالتالي:

تعبئة جدول الحقيقة

لو كان عندنا 4 مداخل للبوابة السابقة تصبح الصفوف(الاحتمالات) 16 صف(احتمال) بدلا من 8 صفوف ؛ويتم تعبئة المداخلA و B و C بنفس الطريقة السابقة ولكن مع زيادة 8 احتمالات، ويكون المدخل الرابع D نبدأ ب 8 احتمالات (0) ثم 8 احتمالات (1).

بوابة AND ثلاث مداخل (المدخل الزائد عن الحاجة في البوابة AND)

في بعض الأحيان تكون البوابة AND لها ثلاث مداخل ولا نريد استخدام سوى مدخلين فقط فماذا نفعل بالمدخل الزائد عن الحاجة؟

من الخطأ جعل هذا الطرف عائم Floating input أو توصيله بالأرضي حيث أن البوابة AND حتى تعمل لابد أن يكون جميع مداخلها تساوي(1)؛ولذلك حتي يتم إلغاء مدخل من مداخل البوابة AND لابد من توصيله ب 5 فولت(Logic 1) أو توصيلة بأخذ المداخل المجاورة له (أي دمج مدخلين مع بعض).

زيادة عدد مداخل البوابة AND

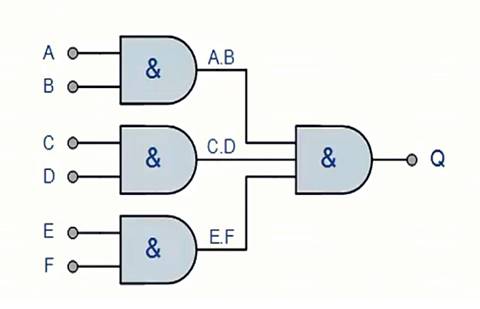
زيادة عدد مداخل البوابة AND

لو عندنا ثلاث بوابات AND لكل واحدة منهما مدخلين ونريد تحويلهم إلي بوابة AND واحدة ب 6 مداخل ومخرج واحد، ويكون ذلك بتوصيل مخرج كل بوابة من البوابات الثلاث بمدخل بوابة AND رابعة تقوم بجمع البوابات الثلاث ويتم الحصول على خرج واحد فقط، قيمة هذا الخرج تساوي Q=(A.B).(C.D).(E.F)

داتا شيت البوابة AND

داتا شيت البوابة AND

سوف نقوم بشرح بعض الكلمات التي نجدها في الداتا شيت والتي تساعدنا على فهم كيفية عمل البوابة AND؛توجد لدينا عائلتين للبوابة AND؛عائلة TTL Logic Types وCMOS Logic Types وهما يختلفان عن بعضهما في نوع الترانزستور المستخدم في تصنيع البوابة.

أهم المصطلحات الموجودة في الداتا شيت للبوابة AND

Quad 2-input :هذا معناه أن داخل الاي سي( IC ) سوف نجد أربع بوابات AND لكل واحدة منهما مدخلين ومخرج واحد ويمكننا استعمال واحدة فقط من هذه البوابات وعدم استخدام الاخريات.
Triple 3-input: هذا معناه أن داخل الاي سي( IC ) سوف نجد ثلاث بوابات AND لكل واحدة منهما ثلاث مداخل ومخرج واحد.
Dual 4-input:هذا معناه أن داخل الاي سي( IC ) سوف نجد بوابتان AND لكل واحدة منهما أربع مداخل ومخرج واحد.

يجب مراعاة عند عمل دائرة باستخدام البوابة 74LS08 Quad 2-input يجب توصيل المدخل رقم 14 بباور سبلاي قيمته 5 فولت وتوصيل المدخل رقم 7 بالأرضي لضمان عمل الاي سي( IC ) أو البوابة بشكل سليم الحصول على نتائج صحيحة.

استخدامات البوابة AND

احد استخدامات البوابة AND هو تفعيل أو إيقاف أحد الأنظمة أو الإشارات عن طريق خط التحكم في بوابة AND.

خط التحكم في بوابة AND

يمكن التحكم في نقل البيانات Data من عدمه عن طريق البوابة AND وذلك بربط أحد مداخل البوابة بمفتاح(Switch)عند الإيقاف لا يتم نقل البيانات ويكون المدخل موصل بالأرضي، بينما عند التشغيل يتم نقل البيانات حيث يكون المدخل موصل ب 5 فولت.
تستخدم البوابة AND في تفعيل أو عدم تفعيل نظام العداد.
تستخدم البوابة AND في الحصول على عدد النبضات في الثانية الواحدة (يعمل كمقياس تردد).

 

كلمة أخيرة

أهمية بوابة AND في عالم الإلكترونيات والرقميات هائلة، فهي بمثابة اللبنة الأساسية للعديد من الدوائر والعمليات المنطقية. تعمل بوابة AND كحجر أساس للعمليات المنطقية البسيطة ،كما تعتبر بوابة AND سهلة البناء مقارنة بالبوابات المنطقية الأخرى، ويمكن تنفيذها باستخدام مجموعة متنوعة من التقنيات الإلكترونية. وهذا يجعلها مرنة للغاية ويمكن استخدامها في مجموعة واسعة من التطبيقات.
تتيح بوابة AND للمصممين الإلكترونيين مرونة أكبر في تصميم الدوائر، حيث يمكن استخدامها لإنشاء شروط منطقية محددة ومعقدة.
تعد بوابة AND عنصرًا أساسيًا في مجال الالكترونيات الرقمية، حيث تلعب دورًا حيويًا في تنفيذ العمليات المنطقية، بناء الدوائر المعقدة، توفير المرونة والتحكم، سهولة الاستخدام.

مراجع
دورة الالكترونيات الرقمية: البوابات المنطقية - بوابة AND، ومراجع أخرى.