ما هو الجبر البولي Boolean Algebra
تعريف الجبر البولي ؟
الجبر البولي هو قسم من الرياضيات يتعامل مع العمليات على القيم المنطقية ويتضمن المتغيرات الثنائية، والعامل المميز للجبر البولي هو أنه يتعامل فقط مع دراسة المتغيرات الثنائية مع القيم المحتملة 1 (صواب) أو 0 (خطأ)،يُعرف الجبر البولي أيضًا باسم الجبر الثنائي.
ويُعتَبر فرعاً من فروع الجبر حيثُ يعمل بمُتغيّرين اثنين هما الصح أو الخطأ ويُرمز لهما بالعددين 1 و 0 بعكس الجبر الابتدائي الذي قد يكون المُتغيّر فيه أي عددٍ كان. وفي حين أن العمليّات الرئيسيّة في الجبر هي الجمع والضرب، تكون العمليّات في الجبر البولي هي العطف أو الوصل (بالإنجليزية: Conjunction) وتُقرأ على أنّها واو العطف ( وَ and) ويُرمز لها بالرمز ∧؛ والعمليّة الثانية هي الفصل (بالإنجليزية: Disjunction) وتُقرأ على أنّها حرف التخيير (أو or) ويُرمز لها بالرمز ∨؛ وثالث العمليّات الرئيسيّة هي النفي (بالإنجليزية: Negation) (ليس not) ويُرمز لها بالرمز ¬. وبهذا، تكون العلاقات في الجبر البولي مُشابِهة للعلاقات العددية المستخدمة في الجبر المعتاد.
تحويل المعادلات الجبرية إلى دوائر منطقية
وحتى نتعرف أكثر على الجبر البولي سوف نفترض بالمثال التالي:
 |
| تحويل المعادلات الجبرية إلى دوائر منطقية |
نفترض أن لدينا نظام سيارة Car System لديه بعض المجسات مثل مجس الحرارة Temperature Sensor ومجس للوقود Fuel Level ومجس لجهد البطارية Battery Voltage ومجس لمستوى الزيت Oil Level هذه المجسات عندما تكون عند مستوي معين يعمل محرك السيارة أو لا يعمل وهذا هو الخرج (حالة محرك السيارة Engine State).
وفي النظام الرقمي يتم التعبير عن قيم المجسات الأرقم 0 ،1 فنجد التالي:
المدخلات Input
مجس الحرارة Temperature Sensor⬅ في حالة الحرارة المرتفعة High يساوي 1، وفي حالة الحرارة المنخفضة Low يساوي 0.
مجس الوقود Fuel Level⬅ في حالة كان مستوى الوقود جيد Good يساوي 1، وفي حالة كان مستوى الوقود منخفض Low يساوي 0.
جهد البطارية Battery Voltage⬅ في حالة كان جهد البطارية كبير أو جيد High يساوي 1، وفي حالة كان جهد البطارية ضعيف Low يساوي 0.
مستوى الزيت Oil Level⬅ في حالة كان مستوى الزيت جيد Good يساوي 1، وفي حالة حالة كان مستوى الزيت منخفضLow يساوي 0.
المخرجات Output
حالة محرك السيارة Engine State⬅في حالة أن يعمل On يساوي 1، وفي حالة عدم عمله Off يساوي 0.
كيف يتم صنع القرار؟
تعمل السيارة عندما تكون الحرارة منخفضة (يعني تساوي 0) وهو الدخل A، و مستوى الوقود جيد (يساوي 1) وهو الدخل B، ومستوى الزيت جيد (يساوي 1) وهو الدخل C، وجهد البطارية عالي (يساوي 1) وهو الدخل D.
فيصبح لدينا الخرج Q يساوي (1) عندما يكون A يساوي 0 وB يساوي 1 وC يساوي 1 وD يساوي 1.
ملاحظة نجد الدخل A فوقه شرطة وهذا يعني ان متصل بوابة نفي Not gate لتحويله من 0 إلى 1 لكي تعمل البوابة بشكل صحيح.
 |
| إضافة مدخل التمكين |
لنفترض أنك لديك تعديل على الدائرة السابقة وهذا التعديل يكون بإضافة مدخل جديد يعبر عن التمكين Enable عندما يكون يساوي 1 أو عدم التمكين disable عندما يكون يساوي 0 ويرمز له بالرمزE، وهذا التعديل يمنحك عمل السيارة بالرغم من مستوى الوقود او الزيت يكون منخفض عندما يكون هذا المدخل في وضع التمكين، ومما سبق نستنتج أن عندما يكون هذا المدخل في وضع التمكين (يساوي 1) تكون جميع المدخلات الأخرى تساوي 1 بغض النظر عن حالتها وتعمل السيارة والعكس عندما يكون هذا المدخل يساوي 0.
كيفية تحويل دائرة منطقية إلى معادلة الجبر البوليني
 |
| كيفية تحويل دائرة منطقية إلى معادلة الجبر البوليني |
لتحويل أي دائرة منطقية إلى معادلة الجبر البوليني عليك أن تبدأ من المدخلات في
أقصى اليسار متجه إلى الخرج النهائي للدائرة وذلك بكتابة الخرج لكل بوابة.
وفي الشكل السابق يمكن لنا استنتاج التعبير البوليني لهذه الدائرة كما يلي:
التعبير البوليني لبوابة AND والتي لها الدخلان A ،NOT B وبالتالي يكون الخرج هو A.NOT B
التعبير البوليني لبوابة AND والتي لها الدخلان NOT A ،C ويكون الخرج هو NOT A .C
ويكون التعبير البوليني لبوابة OR والتي لها الدخلان A.NOT B و NOT A .C يكون الخرج لها A.NOT B + NOT A .C
وبناء على ما سبق يكون الخرج النهائي للدائرة هو Y=AB¯ + ĀC
عند تصميم أي دائرة منطقية يجب مراعاة أن تكون عدد البوابات المستخدمة أقل ما يمكن، مع أقل عدد ممكن من المدخلات لكل بوابة وذلك لتوفير التكاليف المطلوبة لتصميم الدائرة.
سوف نتناول فيما يلي تبسيط الدوال المنطقية (التعبيرات البولينية) باستخدام قواعد الجبر البوليني.
القاعدة رقم 1⬅A+1=1
في هذه القاعدة إذا كان أحد الدخلين لبوابة OR دائما يساوي (1) والدخل الآخر A، والذي يأخذ القيمة (1) أو القيمة (0). وجود (1) على أحد الدخلين لبوابة OR يعطي دائما خرج يساوي (1) بغض النظر عن قيمة المتغير الذي على الدخل الآخر، وبناء على ذلك فان أي متغير يدخل على بوابة OR مع (1) فإن الخرج دائما يساوي (1).
القاعدة رقم 2⬅A+0=A
هذه القاعدة يمكن فهمها بملاحظة ماذا يحدث عندما يكون أحد الدخلين لبوابة OR دائما يساوي (0) والدخل الآخر هو A، والذي يمكن أن يأخذ القيمة (1) أو (0)، فإذا كان A=1 فإن الخرج يساوي (1) وهو بذلك يساوي A، وإذا كان A=0 فإن الخرج يساوي (0) وهو أيضا يساوي A، وبناء على ذلك فإن أي متغير يدخل على بوابة OR مع (0) فإن الخرج يساوي قيمة هذا المتغير.
القاعدة رقم 3⬅A.1=A
إذا كان أحد الدخلين لبوابة AND دائما يساوي (1) والدخل الآخر A، فإن الخرج يساوي قيمة المتغير (A)، فاذا كان المتغير A=0 فإن خرج البوابة AND يساوي (0)، وإذا كان المتغير A=1 فإن خرج البوابة AND يساوي (1) لأن الدخلين الآن قيمتهما تساوي
(1)k وبناء على ذلك فإن أي متغير يدخل على بوابة AND مع (1) فإن الخرج يساوي قيمة هذا المتغير.
القاعدة رقم 4⬅A.0=0
إذا كان أحد الدخلين لبوابة AND دائما يساوي (0) والدخل الآخر A، فإن الخرج دائما يساوي (0) بصرف النظر عن قيمة المتغير الذي على الدخل الآخر، وبناء على ذلك فان أي متغير يدخل على بوابة AND مع (0) فان الخرج دائما يساوي (0).
القاعدة رقم 5⬅A+A=A
إذا كان كل من الدخلين للبوابة OR عليهما نفس المتغير A، فإن الخرج يكون قيمة هذا المتغير، فاذا كان المتغير A=0 فذلك يعني (0+0=0)، وإذا كان المتغير A=1 فذلك يعني (1+1=1).
القاعدة رقم 6⬅A.A=A
إذا كان كل من الدخلين للبوابة AND عليهما نفس المتغير A، فإن الخرج يكون قيمة هذا المتغير، فاذا كان المتغير A=0 فذلك يعني (0.0=0)، وإذا كان المتغير A=1 فذلك يعني (1.1=1)، وفي كلتا الحالتين يكون خرج البوابة AND يساوي قيمة المتغير A.
القاعدة رقم 7⬅ NOT NOT A=A
إذا تم عكس متغير مرتين تكون النتيجة هي قيمة هذا المتغير. إذا كان المتغير =0 A وتم عكسه نحصل على (1)، فإذا تم عكس (1) مرة أخرى نحصل على (0) وهو يساوي قيمة المتغير الأصلي.
القاعدة رقم 8⬅ A +NOT A=1
إذا دخل متغير A على أحد دخلي بوابة OR والمتغير NOT A على المدخل الآخر لنفس البوابة فإن الخرج دائما يساوي (1) حيث أن بوابة OR يكون الخرج لها يساوي 1 إذا كان أحد المداخل لها يساوي 1.
القاعدة رقم 9⬅ A .NOT A=0
إذا دخل متغير A على أحد دخلي بوابة AND والمتغير NOT A على المدخل الآخر لنفس البوابة فإن الخرج دائما يساوي (0)، وهذا من السهل فهمه لأن أحد الدخلين A أو NOT A سوف يساوي (0) دائما، وعندما يوجد (0) على أحد دخلي بوابة AND فمن المؤكد أن الخرج يساوي (0) أيضا.
تستخدم نظريات ديمورجان لتحويل التعبيرات الجبرية من وضعية AND الأساسية إلى وضعية OR وبالعكس، كما تسمح
لنا بحذف العلامات الفوقية (bars) من المتغيرات المتعددة.
وفي الشكل السابق يمكن لنا استنتاج التعبير البوليني لهذه الدائرة كما يلي:
التعبير البوليني لبوابة AND والتي لها الدخلان A ،NOT B وبالتالي يكون الخرج هو A.NOT B
التعبير البوليني لبوابة AND والتي لها الدخلان NOT A ،C ويكون الخرج هو NOT A .C
ويكون التعبير البوليني لبوابة OR والتي لها الدخلان A.NOT B و NOT A .C يكون الخرج لها A.NOT B + NOT A .C
وبناء على ما سبق يكون الخرج النهائي للدائرة هو Y=AB¯ + ĀC
تبسيط معادلات الجبر البوليني (تبسيط التعبيرات البولينية باستخدام الجبر البوليني)
عند تصميم أي دائرة منطقية يجب مراعاة أن تكون عدد البوابات المستخدمة أقل ما يمكن، مع أقل عدد ممكن من المدخلات لكل بوابة وذلك لتوفير التكاليف المطلوبة لتصميم الدائرة.
سوف نتناول فيما يلي تبسيط الدوال المنطقية (التعبيرات البولينية) باستخدام قواعد الجبر البوليني.
قواعد الجبر البوليني Rule of Boolean Algebra
القاعدة رقم 1⬅A+1=1
في هذه القاعدة إذا كان أحد الدخلين لبوابة OR دائما يساوي (1) والدخل الآخر A، والذي يأخذ القيمة (1) أو القيمة (0). وجود (1) على أحد الدخلين لبوابة OR يعطي دائما خرج يساوي (1) بغض النظر عن قيمة المتغير الذي على الدخل الآخر، وبناء على ذلك فان أي متغير يدخل على بوابة OR مع (1) فإن الخرج دائما يساوي (1).
القاعدة رقم 2⬅A+0=A
هذه القاعدة يمكن فهمها بملاحظة ماذا يحدث عندما يكون أحد الدخلين لبوابة OR دائما يساوي (0) والدخل الآخر هو A، والذي يمكن أن يأخذ القيمة (1) أو (0)، فإذا كان A=1 فإن الخرج يساوي (1) وهو بذلك يساوي A، وإذا كان A=0 فإن الخرج يساوي (0) وهو أيضا يساوي A، وبناء على ذلك فإن أي متغير يدخل على بوابة OR مع (0) فإن الخرج يساوي قيمة هذا المتغير.
القاعدة رقم 3⬅A.1=A
إذا كان أحد الدخلين لبوابة AND دائما يساوي (1) والدخل الآخر A، فإن الخرج يساوي قيمة المتغير (A)، فاذا كان المتغير A=0 فإن خرج البوابة AND يساوي (0)، وإذا كان المتغير A=1 فإن خرج البوابة AND يساوي (1) لأن الدخلين الآن قيمتهما تساوي
(1)k وبناء على ذلك فإن أي متغير يدخل على بوابة AND مع (1) فإن الخرج يساوي قيمة هذا المتغير.
القاعدة رقم 4⬅A.0=0
إذا كان أحد الدخلين لبوابة AND دائما يساوي (0) والدخل الآخر A، فإن الخرج دائما يساوي (0) بصرف النظر عن قيمة المتغير الذي على الدخل الآخر، وبناء على ذلك فان أي متغير يدخل على بوابة AND مع (0) فان الخرج دائما يساوي (0).
القاعدة رقم 5⬅A+A=A
إذا كان كل من الدخلين للبوابة OR عليهما نفس المتغير A، فإن الخرج يكون قيمة هذا المتغير، فاذا كان المتغير A=0 فذلك يعني (0+0=0)، وإذا كان المتغير A=1 فذلك يعني (1+1=1).
القاعدة رقم 6⬅A.A=A
إذا كان كل من الدخلين للبوابة AND عليهما نفس المتغير A، فإن الخرج يكون قيمة هذا المتغير، فاذا كان المتغير A=0 فذلك يعني (0.0=0)، وإذا كان المتغير A=1 فذلك يعني (1.1=1)، وفي كلتا الحالتين يكون خرج البوابة AND يساوي قيمة المتغير A.
القاعدة رقم 7⬅ NOT NOT A=A
إذا تم عكس متغير مرتين تكون النتيجة هي قيمة هذا المتغير. إذا كان المتغير =0 A وتم عكسه نحصل على (1)، فإذا تم عكس (1) مرة أخرى نحصل على (0) وهو يساوي قيمة المتغير الأصلي.
القاعدة رقم 8⬅ A +NOT A=1
إذا دخل متغير A على أحد دخلي بوابة OR والمتغير NOT A على المدخل الآخر لنفس البوابة فإن الخرج دائما يساوي (1) حيث أن بوابة OR يكون الخرج لها يساوي 1 إذا كان أحد المداخل لها يساوي 1.
القاعدة رقم 9⬅ A .NOT A=0
إذا دخل متغير A على أحد دخلي بوابة AND والمتغير NOT A على المدخل الآخر لنفس البوابة فإن الخرج دائما يساوي (0)، وهذا من السهل فهمه لأن أحد الدخلين A أو NOT A سوف يساوي (0) دائما، وعندما يوجد (0) على أحد دخلي بوابة AND فمن المؤكد أن الخرج يساوي (0) أيضا.
نظرية ديمورجان
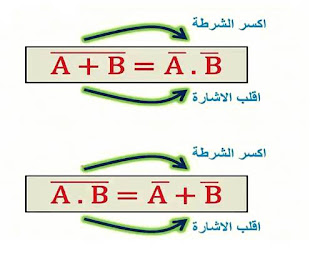 |
| نظرية ديمورجان |
تستخدم نظريات ديمورجان لتحويل التعبيرات الجبرية من وضعية AND الأساسية إلى وضعية OR وبالعكس، كما تسمح
لنا بحذف العلامات الفوقية (bars) من المتغيرات المتعددة.
المصادر

