
|
| ما هي خريطة كارنوف Karnaugh Map |
خريطة كارنوف Karnaugh Map
هي وسيلة لتبسيط واختصار التوابع المنطقية من خلال تبسيط التعابير والعلاقات بطريقة منظمة للحصول على أبسط تعبير ممكن.
ويتكون هذا المخطط أساساً من جدول حقيقة صمم لتحديد التعبير المنطقي الأصغر لمجموع جداءات تابع منطقي.
في العديد من الدوائر الرقمية والمسائل العملية، نحتاج إلى إيجاد تعبيرات ذات
أقل قدر من المتغيرات. يمكننا تصغير التعبيرات المنطقية المكونة من 3 أو 4
متغيرات بسهولة شديدة باستخدام خريطة كارنوف K-map دون استخدام أي من
نظريات الجبر البوليني.
التبسيط باستخدام خريطة كارنوف Karnaugh Map
|
| التبسيط باستخدام خريطة كارنوف Karnaugh Map |
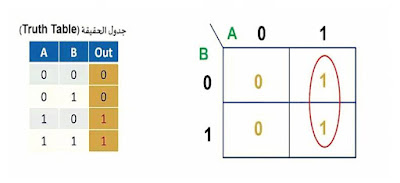
حتى نتعرف على خطوات التبسيط باستخدام خريطة كارنوف Karnaugh Map نفترض أن لدينا جدول حقيقة Truth Table له مدخلين Input هما A و B تم تعبئة جدول الحقيقة بالطريقة المعتادة لتعبئته،حتى نحوله إلى خريطة كارنوف نقوم برسم مستطيل أو مربع له ضلعان الضلع الأول له يعبر عن الدخل A وتكون القيم التي يحتوي عليها هذا الضلع هي 0 و 1 ويتم تقسيم هذا الضلع إلى قسمين قسم يعبر عن القيمة 0 والقسم الاخر يعبر عن القيمة 1، والضلع الثاني يعبر عن B وتكون القيم التي يحتوي عليها هذا الضلع هي 0 و 1 ويتم تقسيم هذا الضلع إلى قسمين قسم يعبر عن القيمة 0 والقسم الاخر يعبر عن القيمة 1 أيضا.
داخل المربع المرسوم سوف تكون قيمة الخرج Output ونحصل عليه من خلال جدول الحقيقة السابق بتطبيق قيم كلا من A و B به ومعرفة قيمة الخرج ويكون كالتالي:
عندما يكون A = 0 وB =0 ⬅ الخرج Output =0
عندما يكون A = 0 وB =1 ⬅ الخرج Output =0
عندما يكون A = 1 وB =0 ⬅ الخرج Output =1
عندما يكون A = 1 وB =1 ⬅ الخرج Output =1
وبعد ما حصلنا على قيم الخرج وقمنا بعمل خريطة كارنوف نقوم بالنظر إلى قيم (1) للخرج وإهمال قيم الخرج(0)،ونقوم بعمل تجميع للقيم (1) في حلقات أفقية أو عامودية ومعنى هذا أن هذه القيم لابد أن تكون متجاورة وليست بعيدة عن بعضها البعض(بشكل قطري)،
خطوات التبسيط (الاختصار او الاختزال) للتعابير البولينية باستخدام خريطة كارنوف Karnaugh Map
يمكن لنا مما سبق نستنتج معا خطوات التبسيط للتعابير البولينية باستخدام خريطة كارنوف كما يلي:
1- نرسم مربع أو مستطيل (رسم خريطة كارنوف على حسب عدد المداخل)

|
| رسم خريطة كارنوف على حسب عدد المداخل |
لو كان لدينا مدخلين A وB يكون أحد الاضلاع هو المدخل A والضلع الاخر هو B ونرسم مربع،أما إذا كان لدينا ثلاث مداخل A وB وC يكون أحد الأضلاع هو AB والضلع الاخر هو C ونرسم مستطيل،أما إذا كان لدينا أربع مداخل A وB وC وD يكون أحد الأضلاع هو AB والضلع الاخر هو CD ونرسم مربع.
تكون القيم عندما يكون لدينا مدخلين فقط هما (0 ،1)،أما عندما يكون لدينا ثلاث أو أربع مداخل تكون القيم للمداخل هي (00،01،11،10) ،يجب ملاحظة أن الخلايا المتجاورة يجب أن تختلف في بت(bit) واحد فقط.
2- نرسم حلقة أو حلقات لتجمع مجموعة من (1) ولكن بشرطين:
- أن تكون قيم (1) متجاورة في وضع أفقي أو عامودي فقط.
- يجب أن يكون عددها (القيم داخل الخلية) هو 16،8،4،2،1،......
3- التعبير عن كل حلقة بتعبير بوليني جديد
فكل قيمة (1) في التعبير البوليني تكون Minterms لوحدها ولكن في خريطة كارنوف يتم جمع قيم (1) في نفس الحلقة للحصول على Minterm واحد لها،فنجد مثلا أنه في المثال السابق لدينا 2 Minterms في التعبير البوليني ولكن في خريطة كارنوف تكون قيمة الخرج ل A في الحلقة هي (1) أما B فمن الممكن أن تكون (1) أو أن تكون (0) ولذلك يتم الاستغناء عن الدخل B ولذلك يكون الخرج هو A فقط وبذلك يكون التبسيط.
تمارين على خريطة كارنوف Karnaugh Map
سوف نستعرض بعض التمارين على خريطة كارنوف Karnaugh Map حتى نلم بكل تفاصيل التبيسط باستخدام خريطة كارنوف Karnaugh Map وتثبيت كافة المعلومات بالتطبيق العملي لها.
تمرين 1 على خريطة كارنوف Karnaugh Map
نفترض أن لدينا جدول حقيقة بثلاث مداخل كما يلي:

|
| جدول حقيقة بثلاث مداخل |
تبسيط جدول الحقيقة بثلاث مداخل باستخدام خريطة كارنوف
نقوم بتبسيطه باستخدام خريطة كارنوف برسم مستطيل حد الأضلاع هو AB وتكون قيمه هي (00،01،11،10)،والضلع الاخر هو C
وتكون قيمه هو (0 ،1)،ويتم نقل قيم جدول الحقيقة بما يقابلها في خريطة كارنوف فنجد مثلا:
عندما يكون A = 0 وB =0 و C=0 ⬅ الخرج Output =0
عندما يكون A = 0 وB =0 و C=1 ⬅ الخرج Output =1
عندما يكون A = 0 وB =1 و C=0 ⬅ الخرج Output =1
عندما يكون A = 0 وB =1 و C=1 ⬅ الخرج Output =0
وهكذا حتى يتم تعبئة خريطة كارنوف Karnaugh Map،ثم نقوم بتجميع الحلقات سوف نجد ان لدينا حلقة متجاورة مكون من قيمتين (1)،ونجد أن هناك خليتين في الاطراف تعتبرهما خريطة كارنوف خلايا متجاورة (تعتبرها كأنها اسطوانة) ويمكن لنا تجميعهم أفقيا في خلية واحدة.
يكون استخراج قيمة Minterms لخريطة كانوف كالتالي:
اول حلقة قيمة A يمكن أن تكون 0 أو 1 فنهملها وقيمة B هي 1 وقيمة C تساوي 0، ولذلك يكون Minterm لهذه الحلقة هو Output =B.not C
ثاني حلقة قيمة A يمكن أن تكون 0 أو 1 فنهملها وقيمة B هي 0 وقيمة C تساوي 1، ولذلك يكون Minterm لهذه الحلقة هو Output =not B.C.
تمرين 2 على خريطة كارنوف Karnaugh Map
|
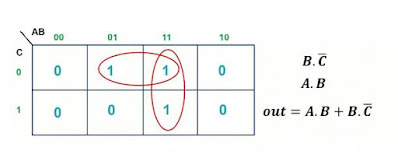
| تمرين 2 على خريطة كارنوف Karnaugh Map |
نجد في هذه الخريطة ثلاث قيم 1 لا يمكن لنا تجميع الثلاثة معا،ولكن يمكن لنا تجميع حلقة أفقية أما القيمة (1) المتبقية نجد أن هناك قيمة اخرى تساوي 1 ولكن فوقه من الحلقة السابقة يمكن لنا تجميعها معه في حلقة دون مشاكل كالتالي:
تمرين 3 على خريطة كارنوف Karnaugh Map
|
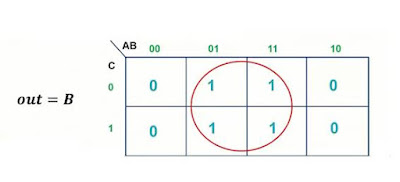
| تمرين 3 على خريطة كارنوف Karnaugh Map |
نجد في هذه الخريطة اربع قيم (1) يمكن لنا تجميعهم معا في حلقة واحدة حيث أن عددهم هو 4 فيمكن لنا جمعهم في حلقة واحدة.
تمرين 4 على خريطة كارنوف Karnaugh Map

|
| تمرين 4 على خريطة كارنوف Karnaugh Map |
نجد في هذه الخريطة اربع قيم (1) يمكن لنا تجميع كل اثنين متجاورين معا في حلقة واحدة،نجد أن لدينا حلقة عامودية وأخرى أفقية.
ملاحظات
حاول تختار أقل عدد من الحلقات وتغطي كل الوحايد.
كلما زاد عدد الحلقات زاد عدد البوابات.
كلما زاد حجم الحلقة كلما كان الاختصار أكبر.
الحالات المهملة في خريطة كارنوف (Don't Care Condition)

|
| الحالات المهملة في خريطة كارنوف (Don't Care Condition) |
هي حالات في جدول الحقيقة صعب جدا أن تتحقق أو الخرج عندها لا يهمنا،وللتوضيح أكثر نفترض أن لدينا حساسان للاحساس باتجاه دوران المحرك هما الحساس A للحركة يمين والحساس B للحركة يسار،فإذا كانت قيمة A وB هي (0) هذا معناه ان المحرك لا يعمل،وإذا كانت قيمة A = 1 وقيمة B =0 هذا معناه ان المحرك تحرك يمين ،وإذا كانت قيمة A = 0 وقيمة B =1 هذا معناه ان المحرك تحرك يسار،ولكن ليس من المعقول أن يتحرك المحرك في الاتجاهين معا ولذلك عندما تكون قيمة A وB تساويان 1 (هي حالة لايمكن أن تحدث) نرمز بالرمز X للخرج،ولكن كيف نرسم خريطة كارنوف لها؟
نرسم خريطة كارنوف بالطريقة المعتادة ويمكن لنا الاستفادة من قيمة X بعمل حلقة كبيرة بالتعويض عنها أو إعتبارها تساوي (1) بما يخدم تكبير الحلقة وتقليل عدد البوابات.
مراجع
دورة الالكترونيات الرقمية للمهندس وليد عيسى :خريطة كارنوف Karnaugh Map
Introduction of K-Map (Karnaugh Map)
مقررات التعليم السوري.


